«- А король то голый!»
Г.Х. Андерсен
Новая натуральная теория относительности явилась
плодом многолетних рассуждений над теорией относительности Эйнштейна.
В позапрошлом веке в результате опыта Майкельсон установил, что скорость света одинакова относительно любых движущихся точек. Это парадоксальное явление природы требовало научного объяснения. Классическая механика в этом вопросе, как известно, оказалась бессильна. Выдвигались несколько гипотез, объясняющих результаты опыта Майкельсона-Морли. Однако все они оказались несостоятельными. Оригинально подошел к разрешению этого вопроса Альберт Эйнштейн, образно говоря, разрубив Гордеев узел. Эйнштейн рассуждая, что если в природе это явление имеет место, значит так и должно быть, положил этот экспериментальный факт как постулат в основу своей теории относительности.
Чтобы придать гармоничность Эйнштейновской теории, который, как теперь уже понятно, является лишь переходным звеном в общей цепи познания истины, этот постулат, сейчас пытаются отождествить с аксиомой в геометрии. Но что такое аксиома?
Аксиома это утверждение, кажущаяся справедливость которого настолько очевидна! что принимается без доказательств.
Нет сомнений в том, что в основе любой естественно научной теории должна лежать система постулатов (аксиомы в физике).
Но под постулатом подразумевается очевидные, элементарные утверждения, подтверждаемые накопленными человечеством наблюдениями и неподдающиеся экспериментальной проверке.
Вспомним теорию Бора о строении атома водорода, в котором явления, требующие научного объяснения, были положены в основу в качестве постулата. Заметим, постулаты Бора не укладывались в рамки понятия постулата. Поэтому такая теория оказалось не в состоянии объяснить строение более сложных атомов. Впоследствии, как мы знаем, в квантовой теории строения атомов, явления, служившие постулатами в теории Бора, получили строгое научное объяснение.
Постулат Эйнштейна о постоянстве скорости света во всех системах отсчета, так же не укладывается в рамку понятия постулата.
Уместно полагаем отметить, что специальная теория Эйнштейна создавалась только для идеальных инерциальных систем отсчета, которых в природе не существует! Поэтому, например, теория Эйнштейна не может объяснить, почему ею предсказанные эффекты возникают и в произвольных системах отсчета. А объяснить простым обобщением выводов специальной теории относительности мы не можем, поскольку всякие другие системы отсчета не являются частным случаем инерциальных систем отсчета, а скорее наоборот. Конечно, надо отдать должное, мы не можем категорично утверждать, что и теория Бора и теория Эйнштейна ошибочны, потому что в принципе эти теории получены как бы методом от противного, т.е. подгонкой под ответ. Тут надо говорить об их относительной истинности, т.е. об их несовершенстве. В частности, такой недостаток возник во временных преобразованиях Лоренца.
В специальной теорий относительности приводятся следующие координатно-временные преобразования для инерциальных систем отсчета К1 и К2.
Если X1О1Y1- неподвижная система координат системы отсчета К1, а X2О2Y2- движущаяся c постоянной скоростью υ система координат системы отсчета К2 (как показано на рисунке 1), то для этих систем отсчета будут иметь место ниже следующие координатно-временные преобразования Лоренца:

где k=скорость света,
х1 и х2 – координаты одной и той же точки соответственно на осях абсцисс систем отсчета К1 и К2.
t1- время движения систем по часам, находящимся в начале системы координат системы отсчета К1,
t2- время движения систем по часам, находящимся в начале системы координат системы отсчета К2.
С формулами (1) и (3) можно согласиться, так как они справедливо допущены изначально и сравнивают длину одного и того же отрезка в двух системах отсчета.
То есть, если в инерциальной системе отсчета К2 расстояние от точки О1 до точки х2 представляют собой х2 +υt2,а в системе отсчета К1 то же расстояние х1, то
х1=γ(х2 +υt2),
где
![]() –
коэффициент Лоренца.
–
коэффициент Лоренца.
И наоборот, если в системе отсчета К1 расстояние от точки О2 до точки х2 представляет собой (х1 - υt1), а в инерциальной системе отсчета К2 то же расстояние х2, то
х2=γ(х1 - υt1).
Из последних двух равенств с помощью алгебраических преобразований получены выражения (2) и(4). Но каков их физический смысл и верны ли физические выводы из них?
Так согласно формуле (2) если в системе отсчета К2 на оси абсцисс в точке х2 имеются часы, то они покажут что время движения в системе отсчета К2
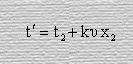
То есть получается, что по часам, расположенным в разных точках на оси абсцисс системы отсчета К2, время движения систем относительно друг друга различно.
Представьте себе длинный поезд, следующий из одного пункта в другой, где пассажиры в конце поезда едут дольше пассажиров, находящихся вначале поезда. Не абсурдна ли такая ситуация?
Или рассмотрим такой пример. Пусть межзвездный корабль в восемь часов утра стартовал с космодрома находящегося на Земле к неподвижной звезде, которая находится от Земли на расстояние 9∙1016м. Через три часа, то есть в одиннадцать часов наблюдатели на Земле обнаружили, что звезда угасла. В какое время это событие произошло на корабле, если скорость корабля 20м/сек.
Очевидно, из временных преобразований Лоренца следует, что время этого события на корабле можно найти из ниже следующего равенства.
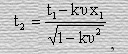
где k=1/c2. Тогда, так как по условию t1=11час, υ=20м/сек, х1= 9∙1016м. и с=3∙108м/сек., получим, что
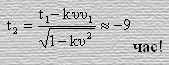
Разве бессмысленность полученного результата говорит о безупречности временных преобразований Лоренца?
В этой новой теории, получены такие же формулы связывающие координаты тела в одной системе с ее координатами в другой, только временные преобразования (2) и (4) выведены немного в ином ниже следующем виде

где k=1/c2,
υ1-скорость тела относительно системы отсчета К1 в точке х1,
υ2 –скорость тела относительно системы отсчета К2 в точке х2.
Применительно к рассматриваемой выше задаче υ1 скорость звезды относительно Земли и υ2– скорость звезды относительно корабля.
Если исходить при решении данной задачи из последних временных преобразований , то мы получим, так как в данном случае υ2=0, что t2 ≈ t1.
С виду идентичные преобразованиям Лоренца координатно-временные преобразования, полученные в данной работе, имеют коренное отличие. Анализ сравнения этих преобразований с преобразованиями Лоренца доказывает определение пространства сформулированного Лобачевским.
Далее в связи с ограниченностью специальной теорий относительности в ней возникает ряд парадоксов. Одним, из которых является знаменитый парадокс близнецов.
Чтобы найти более совершенную модель, описывающую возникающие явления в движущихся системах отсчета, как подсказывает логика, надо исходить из тех же элементарных постулатов классической физики, естественно, исключая не оправдавшийся постулат об абсолютности пространства и времени или, иначе говоря, опираясь на необсолютность пространства.
Поэтому специфика этой натуральной теории заключается в том, что она исходит подобно Римановой геометрии и геометрии Лобачевского из неабсолютности пространства. Такой обобщенный подход к изучению относительного движения дает явные преимущества перед теорией Эйнштейна. Открытые в этой работе соотношения динамичны и, распространяясь на прямолинейное равноускоренное движение, имеют универсальный характер. Выводы же специальной теории относительности здесь могут быть представлены в виде лишь частного случая. Закономерным следствием данной теорий являются не только ограниченность скорости тел и постоянство скорости света, но и теоретическое обоснование, составляющее фундамент квантовой механики, гипотезы де Бройля и закономерный вывод, предположенной на основании многочисленных опытов, формулы Планка. Так же из нее, теоретически вытекают следующие ране установленные на экспериментах факты как сила Лоренца и др. Кроме того, данная теория позволила сделать поправку к Всемирному закону тяготения..
Теперь новый закон Всемирного тяготения, объединяющий гравитационное и ядерное взаимодействия имеет вид.
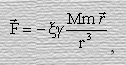
где
![]() –
коэффициент Лоренца, полученный в общем виде (здесь под Е подразумевается
полная энергия, т.е. сумма внутренней Е0, потенциальной Еп
и кинетической Ек энергий).
–
коэффициент Лоренца, полученный в общем виде (здесь под Е подразумевается
полная энергия, т.е. сумма внутренней Е0, потенциальной Еп
и кинетической Ек энергий).
Следствия предоставленной теории позволяют предопределить новую силу, которая возникает в результате движения тел относительно друг друга.
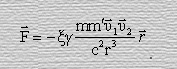
Этой силой объясняется стремление всех планет и галактик к движению в одной плоскости, а также объясняется электрическая природа электронов.
В этой работе так же освещена перспектива осуществления термоядерного реактора стабильно работающего на синтезе ядер.
Теперь единая теория поля, которую предполагал построить Альберт Эйнштейн, и стройная теория микрочастиц, подобная периодической системе Менделеева, уже не за горизонтом.
Подобно математикам, отважившимся признать геометрию Лобачевского, физикам только теперь предстоит сделать шаг по признанию физики, основанной на неабсолютности пространства.