«Теперь, чтобы получить доступ в науку о движении,
нам не надо сперва подниматься на высоты математики;
наоборот, природа сама предстает в своей простой красоте
перед изумленным взором, и даже человек с
небольшими способностями может увидеть множество
вещей, которые до сих пор оставались скрытыми от
величайших ученых»
Роберт Майер (по поводу своего открытого закона сохранения)
Неабсолютность времени
Нет, мы не умаляем заслуги Эйнштейна, его вклад в науку велик. Благодаря нему теперь все уверены в неабсолютности пространства. Потому мы в данной теории исходим из этого обстоятельства, как некогда Лобачевский, опережая событие открытия неабсолютности пространства, построил на этом факторе свою геометрию.
Допустим в системе измерения Z1, из неподвижной точки А прямолинейно и равноускоренно движется тело с начальной скоростью υ0. Учитывая неабсолютность пространства, опишем и сравним движение тела в двух системах отсчета. Собственную систему отсчета К1 данной системы измерения свяжем с материальной точкой А так, чтобы она покоилась в начале координат системы отсчета К1. А вторую систему отсчета К2 свяжем с движущимся телом так же, чтобы оно покоилась в начале ее координат (рис. 4).
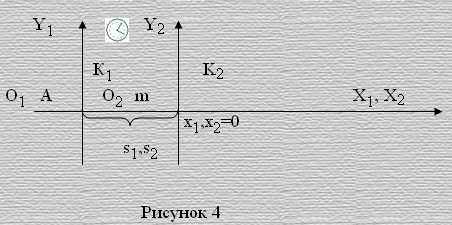
Оси абсцисс систем отсчета, на которых лежит отрезок, соединяющий точку А и тело, направим по направлению движения тела. Будем считать, что оси абсцисс до начала движения были по длине абсолютно идентичными. Длина пройденного пути в данной системе измерения вдоль неподвижной оси О1Х1 будет определяться длиной отрезка О1О2=s1.
где t1 – длительность движения тела по неподвижным часам, находящимся в начале оси О1Х1,
а1- ускорение тела в собственной системе отсчета данной системы измерения.
В силу неабсолютности пространства, мы должны допустить, что длина отрезка О2О1 определяющего длину того же пути в данной системе измерения на движущейся оси О2Х2 будет иметь иное значение, поэтому
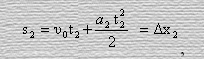
где, под t2 будем предполагать длительность движения тела по часам, находящимся в начале системы отсчета К2.
Оговорим еще раз, что в системе отсчета К2 системы измерения Z1 на оси О2Х2 движется с ускорением а2' точка А, а тело находится в состоянии покоя. Но в данной системе измерения относительно точки А движется тело, следовательно движение этого тела относительно точки А есть и в системе отсчета К2. Или, иначе говоря, движение тела относительно точки А, как событие в силу инвариантности события, есть и в системе отсчета К2. Поэтому мы можем сказать, что ускорение тела в системе отсчета К2 относительно точки А а2 равно а2'. То есть, хотя тело покоится относительно собственных координат системы отсчета К2, мы в то же время говорим, что это тело движется в системе отсчета К2 относительно точки А. В этом выводе, отметим снова, и заключается особенность данной работы.
Таким образом, в данной системе измерения мы имеем для данного тела два значения пройденного пути и времени движения - один на неподвижной оси абсцисс системы отсчета К1, а другой на движущейся оси абсцисс системы отсчета К2.
Найдем отношение длин пройденного пути. Учитывая инвариантность скорости, то есть что
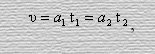(5)
получим
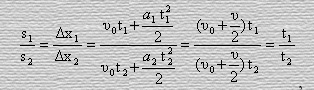(6)
В полученных выражениях наглядно видна пространственно-временная
связь. Если пространство абсолютно. То есть если в данной системы измерения в
один и тот же момент времени в неподвижной системе отсчета и в движущейся
системе отсчета, пройденные пути равны, то и абсолютно время. Если
пространство не абсолютно, то есть если s1
s2,
то и t1t2.
Как видим, из не абсолютности пространства следует и не абсолютность времени.
Попутно следует отметить, что из выражения (5) и (6) можно получить равенство
a1s1=a2s2 (7)
Отсюда видно, что на данный момент времени произведение ускорения на пройденный путь инвариантно.
Коэффициент Лоренца
Далее, так как в целом ввиду однородности пространства, следует, что
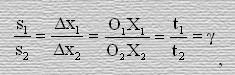(8)
это отношение, равное g, назовем коэффициентом Лоренца.
Коэффициент Лоренца - зависящая от скорости движения величина, которая определяет в данный момент времени каково значение отношения длины неподвижной оси О1Х1 к длине движущейся оси О2Х2 в данной системе измерения, то есть это величина, определяющая количественную меру неабсолютности пространства.
Следует заметить, что если коэффициент Лоренца известен и длина какого либо отрезка в неподвижной системе отсчета равна Δх1, то в движущейся системе отсчета его длина будет
(9)
а если длительность, какого либо процесса в неподвижной системе отсчета, равна t1, то в движущейся системе отсчета длительность этого же процесса будет
(10)
Таким образом, отметим, что, если в неподвижной системе отсчета мы можем непосредственно измерить длину, какого либо отрезка и длительность, какого либо события, то в движущейся системе отсчета данной системы измерения, зная значение коэффициента Лоренца, мы их можем только вычислить. Способ нахождения коэффициента Лоренца выясним позже.
Принцип относительности
Для бесконечных малых изменений положения тела на оси абсцисс за очень малый промежуток времени из формулировок (9) и (10) мы можем получить, что
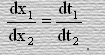(11)
Теперь покажем, что в зависимости от ψ, которой может быть любая переменная физическая величина, из дифференциального уравнения
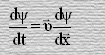(12)
можно получить любой закон.
Пример 1
Пусть требуется найти перемещение движущегося тела, при равноускоренном движении тела. Для этого положим, что в уравнении (12) y =υ – скорость.
Тогда
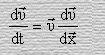(13)
По определению, при равноускоренном движении
-
ускорение, следовательно, из (13) будем иметь
Если в начальный момент движения
x0=0,
а скорость тела равна
то,
интегрируя последнее уравнение, мы придем к выражению
.
Откуда следует формула для нахождения перемещения тела.
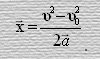(14)
Пример 2
С помощью уравнения (12) мы, в рамках классической механики, можем установить взаимосвязь между импульсом и энергией движущегося тела. Для этого подставим вместо y-функции в уравнений (12) импульс тела р.
Тогда теперь
(15)
По определению импульс тела
поэтому
m=const,
так как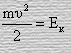 
–
кинетическая энергия получим, что
.
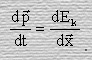Поскольку это отношение по определению является силой F, мы придем к равенству
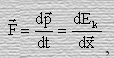(16)
Анализ полученного равенства приведет нас ко второму закону Ньютона и к закону сохранения импульса и энергии.
Пример 3
Пусть в уравнений (12) y = Е, где в пределах классической кинематики Е – полная энергия движущегося тела, то есть Е= Евнутр.+Еk тогда
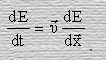(17)
Учитывая, что
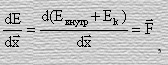
где
,
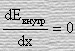а также, что
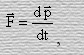
где р – импульс тела.
Выражение (12) преобразуем в следующем порядке
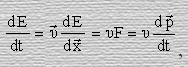
отсюда вытекает важное уравнение динамики
(18)
Пример 4
Если под y в уравнений (12) подразумевать энергию волны ε, то будем иметь
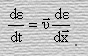(19)
Так как в
таком случае 
вектор
скорости переноса энергии волной, а
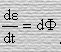-поток
энергии сквозь малую площадку dS
за малый промежуток времени, то мы придем к выводу, что
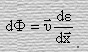
Последнее равенство, поскольку плотность энергии
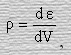
приведем к виду
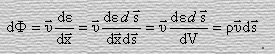
Произведение
(20)
называют вектором Умова, который впервые был введен Н. А. Умовым в 1874 году.
Продолжая рассматривать в рамках дифференциального уравнения (12) и другие переменные физические величины, характеризирующие переменный электрический ток или электромагнитное поле, мы можем пополнить список приводимых примеров. Например, используем вместо функции -y напряженности переменного магнитного и электрического полей. Тогда сразу вытекают электродинамические дифференциальные уравнения:
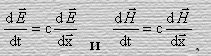(21)
где с – скорость распространения полей.
Следует отметить, что согласно соотношению (11) дифференциальное уравнение (12), будет идентичным во всех системах отсчета. А следовательно все физические законы одинаковы во всех системах отсчета.
Непостоянство массы
Вернемся к рисунку 4. Пусть теперь в системе измерения Z1 из точки А прямолинейно и равноускоренно движется тело под действием постоянной силы F. Силы сопротивления отсутствуют.
Поскольку в данный момент времени длина одного и того же пути, в силу не абсолютности пространства, в рассматриваемых системах отсчета разная, то и затраченная работа в системах отсчета разная. Работа по перемещению тела в данной системе измерения на неподвижной оси абсцисс системы отсчета К1
A1=F1s1 (22)
Аналогично на движущейся оси абсцисс системы отсчета К2
A2=F2s2, (23)
где F1 – сила, действующая на тело в системе отсчета К1, F2 – значение той же силы, в системе отсчета К2.
Ясно, что в данном случае заданная по условию сила, как характеристика движущего тело устройства, одинакова в рассматриваемых системах отсчета.
Действительно, если в системе отсчета К2 есть, к примеру, пружинный динамометр, показывающий величину, действующей на тело силы, то показания этого динамометра будет одним и тем же на протяжений всего заданного времени. Поэтому значение силы при расчете работы в системе отсчета К2 будет равно силе изначально заданной, т.е.
F2=F.
Теперь предположим, что величина силы, действующей на тело, может быть другой только в системе отсчета К1, где в его системе координат тело движется. Произведенная работа в системе отсчета К1 должна быть
А1= F1s1,
Пусть в результате движения сила возрастает или убывает, но тогда в первом случае мы получим выигрыш в работе из ничего, а во втором потерю работы ни во что. В любом случае нарушается закон сохранения энергий, что недопустимо.
Поэтому, одна и та же сила, действующая на рассматриваемое тело в системе отсчета К1 и К2, имеет одинаковое значение, то есть F = F1 = F2. Тогда получим что
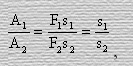(24)
Учитывая выражение (8) будем иметь
(25)
По ходу отметим, что, так как F1=F2, то
(26)
где m1 – масса тела в неподвижной системе отсчета К1, m2 – масса того же тела в движущейся системе отсчета К2.
Из выражения (24) с учетом (7) так же следует и равенство
.
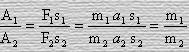Поэтому окончательно будем иметь, что
.
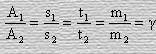(27)
Таким образом, признавая неабсолютность пространства и времени, мы теперь вынуждены признать и изменение в результате движения массы тела.