«Теперь, чтобы получить доступ в науку о движении,
нам не надо сперва подниматься на высоты математики;
наоборот, природа сама предстает в своей простой красоте
перед изумленным взором, и даже человек с
небольшими способностями может увидеть множество
вещей, которые до сих пор оставались скрытыми от
величайших ученых»
Роберт Майер (по поводу своего открытого закона сохранения)
Релятивистский дифференциальный закон сохранения
Выпишем уравнение динамики (18),
![]() (34)
(34)
Масса тела оказалось величиной не постоянной, чтобы учесть это, преобразуем (34) следующим образом
так как
![]() ,
а m =
kE, то
уравнение (34) примет вид
,
а m =
kE, то
уравнение (34) примет вид
![]() (35)
(35)
Отсюда следует равенство
![]() (36)
(36)
Полученное уравнение выражает в рамках механики релятивистский закон сохранения в дифференциальной форме, который можно сформулировать так изменение квадрата импульса прямо пропорционально изменению квадрата внутренней энергии.
Проинтегрировав последнее уравнение (36), будем иметь
![]() (37)
(37)
Так как, при условий p=0 постоянная интегрирования С равна kE02,
где E0 – внутренняя энергия тела до начало движения,
получим
![]() или
или
![]() .
(38)
.
(38)
Из последнего выражения вытекает
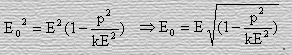 (39)
(39)
откуда следует, что
![]() (40)
(40)
Так как
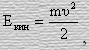 в классической механике кинетическая энергия тела, получим что
в классической механике кинетическая энергия тела, получим что
![]()
Как видим, одной из составляющей внутренней энергий движущегося тела является кинетическая энергия данного тела.
Следовательно, внутренняя энергия движущегося тела Е представляет собой полную энергию тела, движущегося в системе отсчета К1, и в общем случае
![]() (41)
(41)
Тогда, по ходу заметим что, если учесть последнее выражение (41), коэффициент Лоренца в общем случае можно представить в виде
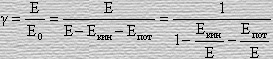 .
(42)
.
(42)
Принимая во внимание равенство (39) установим выражение для коэффициента Лоренца
 (43)
(43)
или
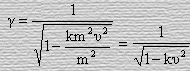
C учетом последнего результата соотношение (32) можем расписать в следующем порядке
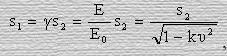 (44)
(44)
, (45)
![]() ,
(46)
,
(46)
Очевидно, что должно выполняться условие
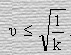 (47)
(47)
Тогда, как видим, скорость тела является величиной ограниченной.
Кинематический вывод формулы для сложения скоростей
Каково же значение k?
Чтобы ответить на этот вопрос, решим следующую задачу.
Пусть три тела начали движение из одной точки вдоль одной прямой относительно друг друга равноускоренно. Начальные скорости тел равны нулю. Допустим, что тела находятся в данный момент времени в точках А, В и С на одной прямой. Свяжем систему координат X1O1Y системы отсчета К1 с телом находящегося в точке А, систему координат X2O2Y2 системы отсчета К2 с телом находящегося в точке В и систему координат X3O3Y3 системы отсчета К3 с третьим телом находящегося в точке С так, чтобы тела покоились соответственно в началах этих систем отсчета (рисунок 5).
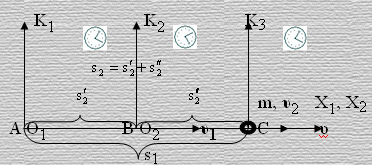
Рисунок 5
Рассмотрим движение относительно системы координат X1O1Y1. Пусть в данный момент времени скорость начала системы координат X2O2Y2 , движущейся по неподвижной оси абсцисс, – υ1, а скорость начала системы координат X3O3Y3, движущейся относительно системы координат X2O2Y2, – υ2 Требуется найти скорость третьего тела в точке С относительно системы координат X1O1Y1.
На рисунке 5 АС=О1С=s1 – длина пути на оси О1Х1, которое проходит третье тело, находящееся в данный момент времени в точке С за время t1 относительно точки А в системе отсчета К1. А s2 = s2'+s2''– длина того же отрезка на оси абсцисс в системе отсчета К2. Прошедшее третьим телом расстояние s2 относительно точки А за время t2 в системе отсчета К2 состоит из длин двух отрезков s2' и s2'', где s2' – расстояние, пройденное началом системы координат X2O2Y2 относительно точки А, и s2'' – расстояние, пройденное третьим телом за то же время относительно начала координат X2O2Y2. Тогда для двух систем отсчета из соотношения (44) следует, что в системе отсчета К1 длина отрезка О1С
![]() (48)
(48)
Если a - ускорение тела, находящегося в точке С относительно точки А в системе отсчета К1, a1- ускорение, с которым движется начало системы координат X2O2Y2 относительно точки А в системе отсчета К2, и a2 – ускорение третьего тела, относительно точки В в системе отсчета К2, то, так как по условию задачи начальные скорости тел равны нулю, соответственно из курса механики имеем
![]() (49)
(49)
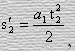 (50)
(50)
![]() (51)
(51)
Тогда, согласно равенству (48), учитывая (49), (50), и (51), будем иметь

или
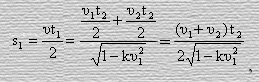 (52)
(52)
где υ – искомая скорость.
В соответствии с выражением (45) для систем отсчета К2 и К3 имеем
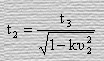 .
(53)
.
(53)
Тогда, продолжая преобразовывать выражение (52), получим
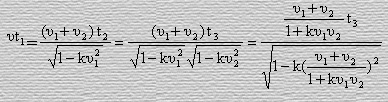 .
(54)
.
(54)
Подобно выражению (53) непосредственно для систем отсчета К1 и К3 мы можем написать равенство
 .
(55)
.
(55)
Сравнивая (54) и (55), приходим к выводу, что
![]() .
(56)
.
(56)
Из полученной формулы для сложения скоростей (56)
следует, что если скорость тела υ2 относительно начало системы
отсчета К2 равна предельной скорости![]() ,
то и относительно начала системы отсчета К1 скорость этого тела так
же равна скорости
,
то и относительно начала системы отсчета К1 скорость этого тела так
же равна скорости![]() ,
то есть, если скорость тела равна предельной скорости, то скорость этого тела
одинакова и равна предельной скорости, относительно любой движущейся точки или
систем отсчета.
,
то есть, если скорость тела равна предельной скорости, то скорость этого тела
одинакова и равна предельной скорости, относительно любой движущейся точки или
систем отсчета.
Тут подводя итог, следует сказать, что полученная формула для сложения скоростей позволяет экспериментально определить значение постоянной - k. Нам известен исторический эксперимент, произведенный в 1881 году Морли – Майкельсоном, из результатов которого следует, что
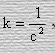
где с – скорость света.
Таким образом, нам надо констатировать постулат Эйнштейна о постоянстве скорости света является закономерным следствием не абсолютности пространства.
Статичный вывод формулы для сложения скоростей
Теперь решим следующую задачу. Пусть энергия и импульс некоторого тела, находящегося в точке С, относительно координат системы отсчета К1 соответственно Е1 и р1, а относительно системы координат системы отсчета К2 соответственно Е2 и р2 (рисунок 6). Какова скорость систем отсчета относительно друг друга?
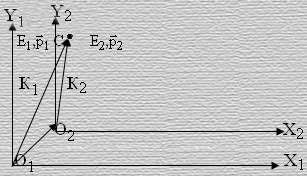
Рисунок 6
В простейшем случае в рамках классической механики скорость систем отсчета относительно друг друга можно найти из равенства
![]() .
(57)
.
(57)
Но релятивистская механика в законе сохранения (36) оперирует квадратом импульса. Да и бесспорно, чтобы искомое уравнение было универсальным, в нем должны учитываться и импульс, и энергия, и масса тела. Поэтому рассмотрим разность квадратов импульсов
![]()
из последнего следует, что
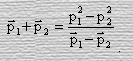
Подставим последнее выражение вместо суммы импульса в числитель формулы (57), тогда искомая скорость
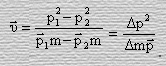 (58)
(58)
К примеру, в классической механике есть выражение
![]() .
Применяя это выражение, найдем скорость систем относительно друг друга.
.
Применяя это выражение, найдем скорость систем относительно друг друга.
После несложных преобразований будем иметь, что искомая скорость
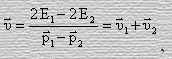 (59)
(59)
где υ1 и υ2 - скорости тела соответственно относительно координат систем отсчета К1 и К2.
Если судить с позиций классической механики, этот результат указывает на справедливость выражения (58). Но каков будет результат, если учесть релятивистскую зависимость энергий от импульса, следующую из выражения (38)?
В связи с тем что
![]()
где Е0 – значение внутренней энергии тела до начала движения, а также, принимая во внимание изменение в результате движения массы тела, из выражения (58) следует, что искомая скорость
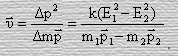 (60)
(60)
Докажем справедливость выражения (60)
Учитывая, что
![]() ,
,
где
![]()
находим, что
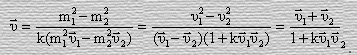 (61 )
(61 )
Если оси абсцисс систем отсчета совпадают, то есть если движение тела происходит на общей оси, то мы придем к выражению (56).
Коэффициент Лоренца
В общем случае выражение (43) можно представить в виде
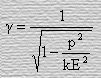
Так как
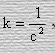 коэффициент Лоренца будет иметь вид
коэффициент Лоренца будет иметь вид
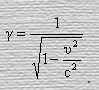
Теперь, умея определять коэффициент Лоренца, перепишем выводы (44),(45),(46),(31),(61)
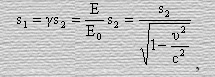 (62)
(62)
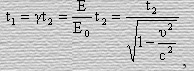 (63)
(63)
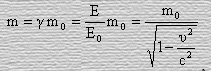 (64)
(64)
![]() (65)
(65)
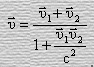 (66)
(66)
Тут надо подметить упругость пространства и времени. То есть необходимо зарегистрировать, что в данный момент времени различие длины одного и того же пути и различие длительности одного и того же движения, а так же в результате движения различие массы данного тела в системах отсчета определяется мгновенным значением скорости систем отсчета относительно друг друга. Иначе говоря, как бы системы не двигались относительно друг друга, соотношения (62) - (64), будут определяться значением скорости систем относительно друг друга в данный момент времени. Следовательно, если скорость систем относительно друг друга обратится в ноль, то при условии отсутствия изменения потенциального поля между телами, пройденный телом путь и время, затраченное им на движение, а так же его масса в системах отсчета станут совершенно одинаковыми. Таким образом, в отношении времени, говорить о парадоксе близнецов, которое уже долгое время поражает воображение фантастов, как видим, теряет смысл.
Далее из (38) следует, что квадрат импульса
![]() .
.
Тогда после несложных преобразований будем иметь
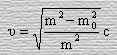 .
.
Полученное означает, что частицы имеющие массу покоя, не могут двигаться со скоростью света.