«Требуемую Евангелием простоту
он доказал всей своей жизнью»
из надгробной надписи на могиле творца
классической механики Исаака Ньютона
Система измерения
В природе существует реальная система измерения, связанная с каким либо телом. В частности, наша система измерения связана с Землей. Под системой измерения будем понимать связанную с телом совокупность всевозможных эталонов измерения (для измерения, например, длины, времени и массы), с помощью которых можно описывать движение любого тела (в том числе и собственного) относительно любой точки (в том числе и движущейся). Так автомобилист, находясь в собственном движущемся автомобиле, может определять его скорость или положение относительно любой точки. Мореходы могут определять свое положение по звездам.
Под эталоном, утвержденным международным научным сообществом в качестве исходного понимается мера или измерительный прибор, служащие для воспроизведения, хранения и передачи единиц, какой либо величины. Например, основная единица массы СИ - килограмм (кг) равен массе международного прототипа, хранимого в Международном бюро мер (в Севре, близ Парижа). Прототип килограмма сделан из платиноиридиевого сплава (90% Рt,10% Ir) в виде цилиндрической гири.
Система отсчета
В системах измерения для описания движения тел используются абстрактные системы отсчета. Под системой отсчета понимается совокупность абстрактной системы координат и часов, связанная с телом, по отношению к которому описываются другие тела. В данной работе для простоты восприятия применяется прямоугольная (декартова) система координат. Более того, в большинстве случаев в данной работе ось ординат в этой системе координат присутствует лишь формально. Поэтому у некоторых, возможно, сложится впечатление примитивности изучения движения. Хотим напомнить, что нет смысла говорить о свойствах пространства и времени, как о нечто таком, что существует само по себе независимо от свойств материй и ее движения. То есть, в данном случае, наличие движущихся тел определяют необходимую для описания размерность пространства. Так если бы мы имели три прямолинейно движущихся тела, не находящиеся на одной прямой, то мы бы описывали движение в двумерном пространстве. А если бы мы имели четыре прямолинейно движущихся тела, не находящиеся на одной плоскости, возникла бы необходимость описания движения в трехмерном пространстве. Но нас интересуют соотношения физических величин только в двух системах измерений, поэтому мы рассматриваем движение только двух тел.
Так как точкой отсчета, в системе измерения может быть любая точка, то таких систем отсчета в одной системе измерения может быть бесчисленное множество.
В системах отсчета данной системы измерения, к примеру, можно определить длину и массу тела или длительности какого либо события. Но под численным значением этих величин будет подразумевать, естественно, значения по отношению к неподвижным эталонам той системы измерения, в котором описывается движение тела.
В системе измерения, систему отсчета, в начале которой покоится данное тело, будем называть собственной системой отсчета этой системы измерения.
Инвариантность движения
Очевидно, что если в системе измерения есть движение, какого либо тела относительно заданной точки, то оно есть в системе измерения не зависимо от выбора систем отсчета. В частности, если в нашей системе измерения Земля вращается вокруг Солнца, то она вращается вокруг Солнца и в системе отсчета связанного с Землей включительно. Только, конечно, надо отметить сложность описания движения Земли в системе отсчета, где Земля находится в покое.
Движение тела относительно заданной точки является одним из видов события. Поэтому инвариантность движения тела относительно заданной точки в системах отсчета данной системы измерения, представляет собой следствие важного свойства события. «Важнейшим свойством события является то, что если событие происходит в какой-либо системе отсчета, то оно обязательно происходит в любой другой системе отсчета».
Пусть в данной системе измерения тело(по рисунку 1) движущееся относительно точки А находится в покое на оси О2Х2 системы отсчета К2. Согласно полученному выше выводу, хотя тело находится в состояний покоя в системе отсчета К2, движение тела относительно точки А, как событие в силу инвариантности события, есть и в системе отсчета К2. То есть, даже если тело покоится относительно собственных координат системы отсчета К2, мы в то же время говорим, что это тело движется в системе отсчета К2 относительно точки А. В этом выводе и заключается особенность данной работы.
Тогда возникает вопрос, как в системе отсчета К2 данной системы измерения можно описать движение тела относительно заданной точки, если оно в системе координат системы отсчета К2 находится в покое?
Разделим рисунок 1 на две системы координат, как показано на рисунке 2 и 3.

На рисунке 2 тело движется относительно точки А в системе координат системы отсчета К1, отметим что положение отправной точки, то есть точки отсчета А в системе координат X1O1Y1 на протяжение всего рассматриваемого события неизменно, а тело движется вдоль оси О1Х1. Отрезок О1О2 на оси О1Х1 есть на данный момент времени пройденный путь в системе отсчета К1.
Мы привыкли к тому, что при описании движения в системе координат начальное положение тела, то есть точки отсчета зафиксировано, а конечное положение тела не постоянно, как на рис.2. Так принято не потому, что по-другому нельзя, а потому что так удобно. Но ведь система координат абстракция. Нам ничто не мешает и никто не может запретить сделать наоборот. Поэтому, поскольку нам требуется описать движение тела относительно точки А в системе отсчета, где тело в его системе координат находится в покое, мы должны принять конечное положение тела фиксированным, а положение точки отсчета переменным как на рисунке 3.
На рисунке 3 относительно точки А мы можем сказать, что тело движется в системе отсчета К2, хотя в его системе координат координаты положения тела неизменны, а движется лишь вдоль оси О2Х2 точка отсчета А. Очевидно отрезок О2О1 на оси О2Х2 на данный момент времени и есть пройденный телом путь в системе отсчета К2.
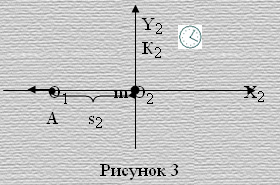
Таким образом, в данной системе измерения мы будем иметь два значения пройденного пути – один в неподвижной системе отсчета, другой в движущейся системе отсчета.
Инвариантность скорости
Из инвариантности движения относительно заданной точки во всех системах отсчета данной системы измерения следует инвариантность скорости движения относительно заданной точки. Действительно предположим, что в данной системе измерения скорость движения тела относительно заданной точки в различных системах отсчета разная. Тогда, так как мы допустили, что скорость тела относительно заданной точки не инвариантна, можно подобрать такую систему отсчета, где скорость тела относительно заданной точки равна нулю. То есть, мы получим систему отсчета, где тело относительно заданной точки находится в покое. Но такой вывод противоречит инвариантности движения относительно заданной точки. Следовательно, относительно заданной точки скорость тела во всех системах отсчета одинакова.
На самом деле, пусть некоторый путник идет пешком по прямой дороге из некоторого населенного пункта, к примеру, со скоростью 5 км/ч. Найдется ли система отсчета, в которой путник будет двигаться относительно этого населенного пункта со скоростью света или вообще относительно этого же населенного пункта будет находиться в состоянии покоя? Очевидно, нет. Путник как шел со скоростью 5 км/ч, так и будет идти с этой скоростью относительно данного населенного пункта в любой системе отсчета данной системы измерения.
Если (по рис. 1) скорости данного тела относительно заданной точки в неподвижной системе отсчета, и в движущейся системе отсчета, в собственной системе координат которой тело покоится, одинаковы, то следовательно, и скорости систем отсчета относительно друг друга в любой момент времени равны друг другу. Как видим, этот вывод созвучен постулату о симметричности пространства.